본 포스팅은 현재 Diffusion model의 기본이 되는 DDPM (Denoising Diffusion Probabilistic Models, 2020, Jonathan Ho, 원문: https://arxiv.org/abs/2006.11239) 을 바탕으로 하나, Diffusion model을 이해하기 위한 기초적인 소개 입니다. 다양한 참고자료를 활용하였으나, 내용 구성 전반의 baseline은 고려대학교 강필성 교수님 유튜브를 참고하였으며, 참고자료는 제일 하단에 명시하였습니다. 제가 잘못 이해한 부분이 있다면 언제든지 댓글 부탁드립니다.
1. Introduction
최근에는 다양한 데이터 형태에서 모든 종류의 deep generative model들이 높은 수준의 샘플들을 생성해낸다. GANs, 자기회귀 모델, flows, VAEs등이 좋은 성과를 보이고 있는데, 이 논문은 diffusion probabilistic model의 발전된 형태를 제시한다. Diffusion model은 마코프 체인에 의해서 파라메터가 결정되며, 샘플을 생성하기 위해 variavational inference(변분 추론)를 이용해 학습 한다. 여기서 마코프 체인은 diffucion process의 reverse로 학습 되는데 diffucion process는 데이터에 점진적으로 노이즈를 추가하는 과정을 말한다. 즉, 마코프 체인은 노이즈가 낀 데이터에서 점진적으로 노이즈가 빠지는 형태를 학습하게 되는 것이다.
Diffusion model은 정의가 쉽고 학습이 효율적이다. 다만 고품질 샘플을 생성할 수 있다는 점이 입증되지 않았는데, 이 논문에서 그것이 가능함을 입증하고자 한다. 특히 diffusion model에 특정한 매개화를 적용하는 경우 다음과 같은 두 가지 등가성을 밝혀냈고, 이것이 논문의 주요 기여 중 하나 이다.
- 학습 과정이 multiple noise에 대한 denoising score matching과 같음
- Diffusion model의 샘플링 과정이 annealed Langevin dynamics와 같음
2. Diiffusion Model

Diffusion model은 기본적으로 원래의 이미지X0에서 조금씩 노이즈가 추가되는 diffusion process와 이 과정을 다시 복원하는 reverse process로 나누어진다.

노이즈가 추가되는 diffusion 과정은 알 수 있으니 q(Xt|Xt−1) 라는 분포로 정의한다면, 그 반대인 노이즈를 제거하는 과정을 pθ(Xt−1|Xt)로 두고 이 파라메터를 추정할 수 있다면 우리는 노이즈에서 새로운 이미지를 생성할 수 있는 것과 같다. (사실 엄밀히 따지면 q(Xt−1|Xt)를 구해야 하지만, 이 값은 추적할 수 없기 때문에 pθ를 이용하여 표현하는 것이다.)
2.1. Diffusion process
노이즈가 추가되는 과정인 Diffusion process는 다음과 같이 정의한다.
q(Xt|Xt−1):=N(Xt;μXt−1,∑Xt−1):=N(Xt;√1−βtXt−1,βt⋅I
자세히 보면 이전 시점(t−1)의 평균과 분산의 정보를 토대로 현재 시점(t)의 상태를 나타낸다고 볼 수 있다. 여기서 β는 노이즈의 주입정도를 말한다. 그리고 β값들의 집합, 즉 노이즈들의 집합을 variance schedule이라고 표현한다. 이 형태에 따라서 Linear scheduling, Sigmoid scheduling, Quadratic scheduling 등이 있는데, 이 논문에서는 T=1000,β0=10−4,β1000=0.02 인 Linear scheduling 모형을 가정하였다. 이 말은 다시 말하면 시간 t가 증가할수록 노이즈가 증가하는 모형이란 뜻이다.
Diffusion process는 자세히 살펴보면 수 많은 Latent variable을 가진 모형이라고 볼 수 있다. X0를 바탕으로 추정한 X1은 하나의 latent variable이 되며, 다시 그 X1을 가지고 만들어낸 X2 역시 latent variable이 될 것이다. 이러한 측면에서 살펴볼 때, 결국 X0를 조건부로 latent variable X1:T를 생성해내는 결합확률분포라고 볼 수 있다.

그러면 최종적으로 diffusion process에 대한 식을 아래처럼 표현할 수 있다.
q(X1:T|X0):=T∏t=1q(Xt|Xt−1)
Reparameterization trick
Xt의 값은 위에서 표현했지만 다음과 같이 쓸 수 있다 → N(Xt;√1−βtXt−1,βt⋅I)
그러나 이전 시점의 정보를 기반으로 한 가우시안 분포를 추출하는 위의 개념으로는 나중에 파라메터를 다시 추적할 수 없다. 즉, backpropagation이 불가능하다.
따라서 이 문제를 해결하기 위해서 reparameterization trick을 사용한다. 이것은 특별한 것이 아니라 해당 분포를 평균과 표준편차로 더해주는 개념이다.
N(Xt;√1−βtXt−1,βt⋅I)=√1−βtXt−1+βtϵt−1
여기서 또 한 가지 알아두고 넘어가야 하는 것이 DDPM의 timestep T는 closed form으로 나타낼 수 있다는 것이다. 이것이 무슨말이냐면 DDPM에서는 T=1000을 가정하므로 1000번의 timestep을 모두 계산하여야 하나 생각할 수 있지만, 이걸 풀어보면 closed form으로 만들 수 있다는 것이다. 이를 위해 αt 라는 변수를 만들어 이것이 1−βt와 같다고 두고 문제를 푸는 것이다. 그렇게 전개를 해보면 최종적으로
Xt=√¯αtX0+√1−¯αtϵ 형태를 얻을 수 있고, 이는 곧 q(Xt|X0) 라는 것을 알 수 있다. 결과적으로 T가 무한히 커진다고 가정하면, √¯αt 는 0에 가까워지고 √1−¯αt 는 1에 가까워지기 때문에 q(Xt|X0) 가 표준 정규분포를 따른다고 볼 수 있다.

2.2 Reverse process
Reverse process는 diffusion process의 역 과정으로, 가우시안 노이즈를 제거해가며 특정한 패턴을 만들어가는 denoising 과정이다.
pθ(X0:T):=p(XT)T∏t−1q(Xt−1|Xt),
pθ(Xt−1|Xt):=N(Xt−1;μθ(Xt,t),∑θ(Xt,t))
Diffusion model의 reverse process 개념을 이해하기 위해서 VAE, Variational Autoencoder와 비교해 볼 수 있다. VAE는 아래와 같이 원본(X)을 넣고 → 원본이 가우시안 분포를 따르는 latent variable (Z)로 변환이 되고 → 이 (Z)가 다시 복원(ˆX) 되는 과정이다. 이 때, 원본과 복원된 이미지 간의 차이를 Reconstruction loss라고 부르고, 우리가 가정한 가우시안 분포가 맞는지 확인하기 위해서 q(Z|X)가 p(Z)와 얼마나 유사한지 확인하기 위한 Regularization term이 존재하며, regularization term은 KL Divergence로 확인한다.

인터넷의 자료 중 VAE는 맨 아래 참고자료 강남우 교수님의 유튜브 영상에 수식에 대한 설명이 매우 자세히 나와있으며, KL Divergence에 대한 설명은 본 블로그에서 다룬적이 있다.
Kullback-Leibler divergence (KL Divergence)
Kullback-Leibler divergence (KL Divergence)
KL Divergence를 이해하기 위해서는 우선 Entropy와 Cross Entropy에 대해서 이해해야 한다. 1. Entropy Entropy의 정의 열의 이동과 더불어 유효하게 이용할 수 있는 에너지의 감소 정도나 무효 에너지의 증가
ai-onespoon.tistory.com
결론적으로 VAE의 loss를 아래처럼 Regularization 부분과 Reconstruction 부분으로 나눌 수 있다면, DDPM은 여기에 denoising process가 추가된 형태라고 할 수 있다. (VAE가 하나의 latent variable Z를 생성했다면, DDPM은 여러 개의 latent variable들을 생성하였기 때문)


2.3. Loss fucntion
논문에서 설명하는 loss function을 따라가기 어려운 부분이 있어서, VAE의 loss에서부터 출발하여 수식을 전개해봤다.
중간의 qϕ(Z|X)는 VAE loss를 계산 가능하게 해주는 핵심 부분이다. 계산이 가능하도록 분자와 분모에 임의로 곱해준 값이다. 어쨌든 이렇게 전개를 하면, ELBO(Evidence Lower BOund) 부분과 KL-divergence구간으로 나뉘는데 KL-divergence 구간에서 pθ(Z|X) 부분을 알 수 없기 때문에 계산이 불가능하다. 다만 KL-divergence 식이므로 0보다 크다는 것을 알기 때문에 ELBO 부분을 최소화 시켜주는 것이 VAE loss 계산의 핵심이라고 할 수 있다.

이걸 토대로 그대로 DDPM에 적용해보면, 아래와 같이 loss function을 얻을 수 있다. 일반적으로 딥러닝의 loss값에서는 최소값을 구하므로 음수를 곱해준다.

그러면 다시 아래와 같이 전개해 볼 수 있는데, 다른 부분은 쭉 따라갈 수 있는데 중간에 네모 표시된 부분에 특이한 점이 있다. 분자에 갑자기 X0가 결합분포로 추가된 것이다. 이것은 마코프 속성의 특성에 기인한다. 마코프 property에 따라 현재 값은 직전 상태에서만 영향을 주기 때문에 최초값을 넣어주어도 결과는 변함이 없다. 물론 안넣어도 변함은 없는데, 이러한 트릭을 사용하는 이유는 이를 통해 베이즈 정리가 가능해지고 결과적으로 계산이 가능해지기 때문이다.

전개가 완료되면 아래와 같은 식을 볼 수 있다. 아래 수식은 DDPM논문과 동일하게 표현하였는데 KL-Divergence 공식에 의하면 regularization term에는 기대값 Eq 가 빠져야 맞는 것 같다. 몇몇 리뷰 논문에서는 기대값을 빼고 작성한 것이 확인된 것으로 보아 아마 DDPM 논문에서의 오타로 추정된다.
여기서 regularization term은 결국 XT시점에서 가우시안분포를 따르는게 맞는냐를 검증하고 싶은 부분이다. 그런데 우리는 diffusion process에서 이미 노이즈가 가우시안 분포를 따른다고 정의했다. 또한 2.1. Diffusion process 부분에서 closed form 형태를 확인할 때, T가 클수록 표준 정규분포에 가까워진다는 것을 증명했으므로 굳이 확인해볼 필요가 없다.
그리고 Reconstruction 부분은 X1이 주어질 때, X0가 발생할 확률인데 DDPM의 timestep 1000 구간에서 하나의 step은 아주 작은 비중을 차지한다. 따라서 해당 부분도 그냥 상수 취급이 가능하다. 결론적으로 우리는 Denoising 부분만 확인하면 된다.

결국 denoising term을 계산해야 하는데 결국 두 확률분포의 KL-divergence를 구하는 부분이다. 먼저 앞 부분인 q(Xt−1|Xt,X0) 부분을 계산하면 아래와 같이 전개가 된다. (여기서 아까 만들어낸 trick이 큰 역할을 한다. Xt−1|Xt는 추론할 수 없지만 X0를 결합 확률분포로 넣어서 베이즈 정리를 통해 식을 다시 정리할 수 있다. 그러면 최종적으로 원본 이미지 X0와 현 시점 이미지 Xt가 있을 때, 평균이 ~μt 이고 분산이 ~βt 인 가우시안 분포를 따른다고 할 수 있다(아래 수식 맨 첫줄). 그리고 ~μt와 ~βt는 수식 맨 아래에서 확인할 수 있다.

그러면 최종적으로 q(Xt−1|Xt,X0) 부분과 pθ(Xt−1|Xt) 부분의 KL-divergence를 구하면 되고, 이는 결국 두 확률분포 기대값의 차이라고 볼 수 있다.

그리고 이것을 전개하면 가장 마지막 최종 loss를 알 수 있다. DDPM은 노이즈 스케쥴을 이용하여 최대한 학습해야 할 파라메터를 간소화하고, loss 역시 매우 간소화했다.
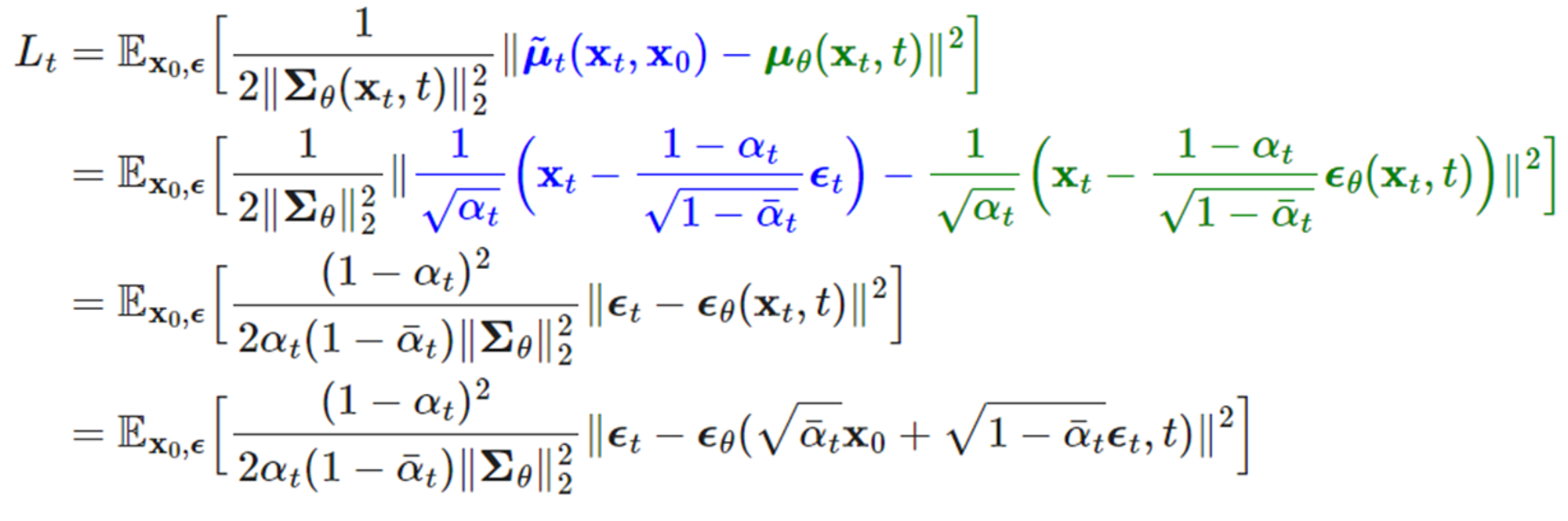

2.4. Trainig
학습은 기본적으로 U-Net 구조로 이루어지며, 논문에서 언급하는 몇 가지 data처리 과정은 생략한다.

3. Experiments
실험 설정
- Weight normalization 대신 group normalization 사용
- Self-attention block 도입
- Time step T의 경우 Transformer에서 도입된 positional encoding을 기반으로 사용
- CIFAR10, LSUN, CelebA-HQ Dataset에 대해 학습 진행
Sample quality
결과에 앞서 정량적 평가지표에 대한 개념은 다음과 같다.

IS(Inception Score) : 생성된 이미지가 명확하게 object를 표현하는지를 나타내는 image quality 값과 다양한 object가 생성되는지 나타내는 image diversity 값 간의 KL Divergence를 기반으로 IS 산출
FID(Frechet Inception Distance) : 사전에 학습된 이미지 분류 모델을 활용해 추출한 feature representation 간 거리(Frechet distance)를 score로 활용
DDPM의 FID는 3.17로 Unconditional 생성 모형 중에서는 가장 좋은 성능을 보인다.
참고
[1] 고려대학교 DSBA (강필성 교수님 연구실) : https://youtu.be/_JQSMhqXw-4?si=L3opz7wUev-aNUoe
[2] 고려대학교 DMQA (김성범 교수님 연구실) : https://youtu.be/Q_o0SpXv9kU?si=K4Pf2QP41IY7UEMI
[3] KAIST 스마트설계연구실 (강남우 교수님 연구실) : https://youtu.be/GbCAwVVKaHY?si=KjyJJUfWss1AMWyH
[4] Lil’Log : https://lilianweng.github.io/posts/2021-07-11-diffusion-models/
[5] https://velog.io/@philiplee_235/Denoising-Diffusion-Probabilistic-Models
'논문리뷰 > Diffusion models' 카테고리의 다른 글
| Stable Diffusion UNet 구조 (0) | 2024.12.19 |
|---|---|
| 통합적 관점에서의 Diffusion model의 이해 (Part 2: VAE) (1) | 2024.12.10 |
| [논문 리뷰] SR3+: Denoising Diffusion Probabilistic Models for Robust Image Super-Resolution in the Wild (0) | 2024.11.21 |
| 통합적 관점에서의 Diffusion model의 이해 (Part 1: 생성 모델의 개념과 ELBO) (0) | 2024.11.20 |
| [논문 리뷰] SR3: Image Super-Resolution via Iterative Refinement (CVPR, 2021) (0) | 2024.05.27 |




댓글