KL Divergence를 이해하기 위해서는 우선 Entropy와 Cross Entropy에 대해서 이해해야 한다.
1. Entropy
Entropy의 정의
- 열의 이동과 더불어 유효하게 이용할 수 있는 에너지의 감소 정도나 무효 에너지의 증가 정도를 나타내는 양
- 정보를 내보내는 근원의 불확실도를 나타내는 양
- 정보량의 기대치를 이르는 말
표준국어대사전에는 위와 같이 entropy를 정의 하였다. 컴퓨터 과학 측면에서는 entropy를 “한 메세지에 들어갈 수 있는 정보량의 비트 수”로 정의 한다. 또한 후술 할 설명에 의하면 entropy는 최적의 정보 전송을 위해 필요한 질문 개수에 대한 기댓값을 의미한다. 조금씩 그 정의에서 차이를 보이긴 하는데, 종합해보면 AI 분야에서의 entropy는 어떤 정보의 양을 나타내는 단위 정도로 이해해 볼 수 있을 것 같다.
정보의 전달 & 측정
정보를 전달 하는 것과 그 정보에 대해서 측정 하는 것은 매우 중요한 문제이다. 예를 들어 다음과 같이 세 가지 정보가 있다고 할 때,
- 10회의 동전 던지기 결과
- 알파벳 6개
- 포커카드 5장
정보를 전달할 때 비용이 발생하는데, 위 세 가지 경우의 정보를 전달 할 때 비용을 어떻게 책정할 수 있을까? 단위도 다 다른데 어떠한 기준으로 어떻게 측정하고 비용을 산출해야 하는 것일까? 이 질문에 대한 대답을 위해 각각의 정보를 전달하는 경우의 수를 생각해보자.
- 10회의 동전 던지기 결과
동전 던지기의 결과는 앞인지 뒤인지를 묻는 질문으로 결과를 알 수 있다. 이진 판별로 1회 결과에 대해 앞이면 1, 뒤면 0이라고 가정하면 1010… 이런식으로 10개의 정보를 전달 할 수 있다. 즉 10개의 질문이 필요하다.
- 알파벳 6개
알파벳은 총 26글자 이다. 이것을 개별적으로 물어본다면 매우 비효율적이다. 예를 들어 알파벳이 B인가요? → NO → K인가요? → NO, 이런식으로 찾아가다 보면 최대 25번의 질문이 필요하다. 그렇다면 이 역시 binary split으로 더 효율적으로 정보를 판별할 수 있다. 가운데가 M이므로 M보다 작냐? 라는 질문을 하고 그게 YES 라면 또 그 절반인 F보다 작냐?… 이러한식으로 질문을 구성하여 split 해보면 4번 혹은 5번이면 정보를 알 수 있다.
이걸 좀 더 수학적으로 써보면
$2^{질문수} = 메세지 공간$
질문이 binary기 때문에 $2^{질문수}$ 를 통해 알고 싶은 정보의 수를 알 수 있다. 위에서 4번 혹은 5번의 split을 통해 알파벳의 정보를 알 수 있다고 했는데, $2^4 = 16,; 2^5=32$ 이므로 4에서 5가지의 질문을 한다는 것은 16~32가지의 정보를 표현할 수 있다는 말이 된다. 알파벳은 26가지의 정보를 가지고 있으니 이 조건에 부합하는 것을 알 수 있다. 다시 수학적 풀이를 해보면 우리는 몇 번의 질문이 필요한 것인지 알고 싶으므로 질문의 수를 $x$로 놓으면
$2^x = 26$
여기서 $x$를 구하기 위해 양변에 밑이 2인 로그를 취한다.
$log_22^x = log_226$
여기서 $x log_22 = x$
$\therefore x = log_226 \approx 4.7$
약 4.7번의 질문으로 알파벳을 찾을 수 있다는 것을 알 수 있다. 그럼 다시 처음 질문으로 돌아가서 알파벳 6개를 전달해야 하므로, $4.7\times 6 = 28.2$ 즉 28.2번의 질문이 필요하다.
- 포커카드 5장
포커카드는 4개의 모양이 13개씩 총 52개의 정보를 가지고 있고, 알파벳을 분기 했던 방식으로 split해보면 5~6번 정도의 정보 전송이 필요하다. 위에서 유도했던 수식으로 전개를 해보면
$2^x = 52$
$x = log_252 \approx 5.7$
포커카드는 5장이므로 $5.7\times5 = 28.5$
총 28.5번의 질문이 필요하다.
정리하면, 위 정보 전달에 대해서 아래와 같은 질문 수가 필요하다.
| 동전 던지기 10회 | 10 |
| 알파벳 6개 | 28.2 |
| 포커카드 5장 | 28.5 |
이 질문의 단위를 1bit라고 하고, 1bit에 1달러의 비용이 필요하다고 가정하면, 각각의 정보 전달에 대해 비용을 청구할 수 있다.
이러한 과정, 즉 정보의 측정을 정리한 사람이 R.V.L Hartley (1928) 이다.
$H(정보) = nlogS = logS^n$
$n$ : 문자, 숫자 등 기호의 수
$S$ : 선택 가능한 기호의 개수
Entropy
Claude Shannon이 정의한 entropy는 불확실성이고, 단위를 bit라고 하였다. 우선 Shannon의 정의한 entropy에 대해서 알아보자.
Machine A와 B가 있고, 각각의 Machine은 알파벳 A, B, C, D를 출력한다고 가정해보자. Machine A는 A, B, C, D를 각각 25%의 확률로 출력한다. Machine B는 A를 50%, B를 12.5%, C를 12.5%, D를 25%의 확률로 출력한다.
$Machine\; A = \begin{cases}P(A) = 0.25 \\ P(B) = 0.25 \\ P(C) = 0.25 \\ P(D) = 0.25 \end{cases}$
$Machine\; B = \begin{cases}P(A) = 0.5 \\ P(B) = 0.125 \\ P(C) = 0.125 \\ P(D) = 0.25 \end{cases}$
각 Machine에서 A, B, C, D의 정보를 얻기 위한 최소한의 질문 개수는 몇 개 일까?
먼저 Machine A의 경우 아래와 같이 젤 먼저 AB가 나오는지 물어보고, 그 뒤로 같은 방식으로 질문을 던질 수 있다.

Binary split 하는 것과 동일하여 어렵지 않게 구분되는 것을 볼 수 있다. 그렇다면 Machine B의 경우는 어떻게 될까? Machine B는 각각의 발생 확률에 차이가 있다. 따라서 그 확률이 절반이 되도록 질문을 해야한다. A의 발생 확률이 50%임으로 제일 처음 질문을 AB가 포함되었는지 묻는 것이 아니고, 그냥 A가 나오는지 물어보면 된다. 그러면 아래와 같은 분류 체계를 확인할 수 있다.

그러면 여기서 질문이 몇 개가 필요할까? Machine A는 고민할 필요 없이 2번의 질문이면 정보를 알 수 있다. 그렇다면 Machine B는?
첫 번째 질문의 결과에서 A가 나온다는 결과를 얻으면 더 이상 질문이 필요 없다. 하지만 A가 나오지 않는 다면 두 번째 질문인 Is it B? 가 또 필요하다. 정리하면 A가 나올 때에는 질문이 1번 필요하고, D가 나올 때에는 질문이 2번 필요하다. C와 D가 나오려면 질문을 3번 해야 한다. 이를 수식으로 써보면,
$P(A)\times 1 + P(D)\times 2 + P(C) \times 3 + P(D) \times 3$
$= 0.5 \times1 + 0.25 \times 2 + 0.125 \times 3 + 0.125 \times 3 = 1.75$
따라서 평균적으로 1.75개의 질문이 필요함을 알 수 있다. Machine A는 2개의 질문이 필요한 반면에, B는 1.75개로 더 적은 질문으로 정보를 전달할 수 있다. 이것이 바로 불확실성이 적기 때문에 발생하는 것이다. 그래서 Shannon은 entropy를 평균적 불확실성의 측정이라고 정의 하고 다음과 같이 표현하였다.
$H = \sum (사건발생확률)\cdot log_2(\cfrac{1}{사건발생확률})$
$= \sum_{i} p_i\; log_2(\cfrac{1}{p_i})$
$= -\sum_{i} p_i\; log_2({p_i})$
위의 Machine 예제와 위 수식을 통해서 entropy는 가능한 모든 사건이 같은 확률로 일어날 때 그 최댓값을 갖는 다는 것을 알 수 있다. 그리고 entropy가 크다는 것은 정보다 많다는 의미가 된다.

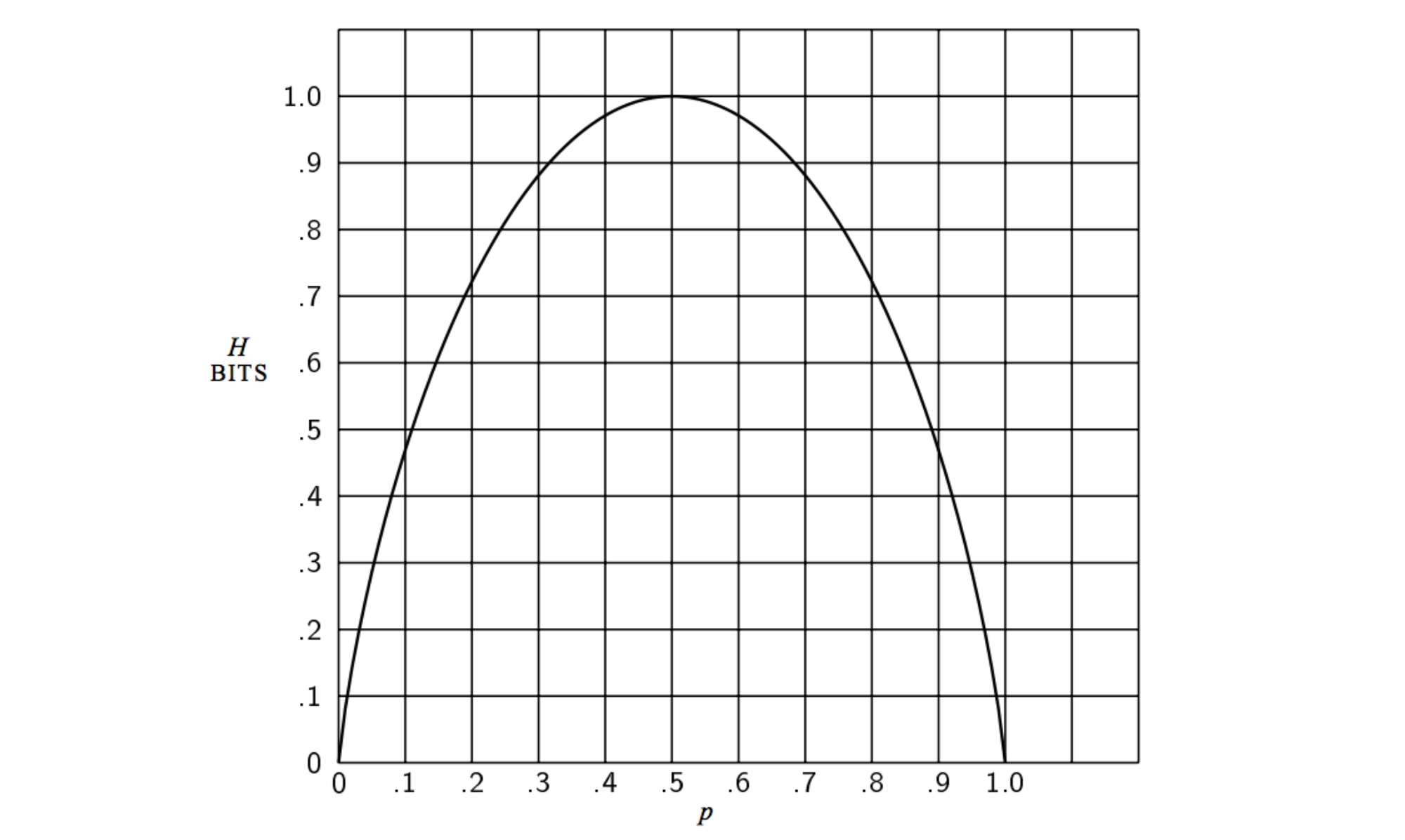
2. Cross entropy
정보이론에서 Cross entropy란 두 확률 분포 $p$와 $q$를 구분하기 위해 필요한 평균 비트 수를 의미한다(위키백과). 정보이론에 대해서 잘 아는 것이 아니라 이 정의에 대해 명확히 해석할 순 없지만, 적어도 AI분야에서는 두 확률 분포 $p$와 $q$의 차이를 나태내는 것으로 이해해 볼 수 있을 것 같다. 그러면 위의 entropy 예제를 통해서 더 자세히 이해해보자.
Cross entropy
Machine A와 Machine B의 entropy 값을 다시 한 번 살펴보자.
$Machine\; A : (0.25 \times 2) \times 4 = 2$
$Machine\; B : 0.5 \times 1 + (0.125 \times 3) \times 2 + 0.25 \times 2 = 1.75$
다시 한 번 보지만 Machine A의 entropy 가 더 크다. Entropy는 최적화된 전략을 가진 상태에서 질문 개수에 대한 기댓값이다. 그런데 여기서 만약 다른 전략을 쓴다면 어떻게 될까? Machine B의 확률을 갖는 값에서 Machine A의 전략을 사용해보자.

이 상태에서 각 확률값을 맞추어 entropy를 계산해보는 것이다. 우선 A가 나올 확률은 0.5인데, 두 번의 질문을 통해서 결과가 발생하므로 $0.5 \times 2$ 임을 알 수 있다. 같은 방식으로 계산해보면,
$0.5 \times 2 + (0.125 \times 2) + 0.25\times2 = 2$
기존에 Machine B의 entropy는 1.75였는데, 더 커진 2가 됨을 알 수 있다. 이것이 바로 cross entropy이다. Cross entropy는 어떤 문제에 대해 특정 전략을 쓸 때 예상되는 질문 개수에 대한 기댓값이며, 여기서 전략은 확률분포로 표현된다. A의 분포를 가지고 B의 결과값을 예측한 것으로도 볼 수 있고, 머신러닝 관점에서 생각해보면 training data set으로 훈련 시킨 parameter들을 test data set에 적용해 본 것으로도 이해할 수 있다. 정리하면 확률분포로 된 어떤 문제 $p$에 대해 확률분포로 된 어떤 전략 $q$를 사용할 때의 질문 개수의 기대값이 cross entropy 이다.
Cross entropy의 사용
Cross entropy를 수식으로 정리하면 다음과 같다.
$H(p, q) = \sum_{i} p_i \; log_2 \cfrac{1}{q_i}$
$=-\sum_{i} p_{i} \; log_2 \;q_{i}$
머신러닝에서 cross entropy를 사용할 때는 $p_i$가 특정 확률에 대한 실제 값이고 $q_i$가 현재 학습한 확률값이다. 위의 Machine 예를 다시 가져오면
$p = [0.5,\; 0.125,\; 0.125,\; 0.25]$
$q = [0.25,\; 0.25,\; 0.25,\; 0.25]$
가 된다. 따라서 우리는 $q_i$를 학습하고 있는 상태에서 이 $q_i$가 $p_i$에 가깝도록 만드는 것이 목표가 되며, $q_i$가 $p_i$에 가까워질수록 cross entropy 값은 작아진다.
3. Kullback-Leibler divergence (KL Divergence)
KL Divergence의 정의
KL Divergence는 두 확률분포의 차이를 계산하는데 사용하는 함수로, 어떤 이상적인 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피 차이를 계산한다. 상대 엔트로피(relative entropy), 정보 획득량(information gain), 인포메이션 다이버전스(information divergence)라고도 한다(위키피디아).
가장 먼저 cross entropy를 전개하면 그 안에 이미 확률분포 $p$의 entropy가 있다는 것을 알 수 있다.
전개를 위해 $p$의 entropy를 더하고 빼줌
$H(p, q) - H(p) + H(p)$ → 이걸 수식으로 표현하면
$H(p, q) = -\sum_{i} p_i\; log\; q_i + \sum_{i} p_i\; log\; p_i - \sum_{i} p_i\; log\; p_i$
→ 원래 $H(p)$는 음수이기 때문에 기호로 된 식과 전개한 수식의 차이를 확인하자
가장 마지막 항 $- \sum_{i} p_i\; log\; p_i$ 를 $H(p)$로 변경해주고 다시 정리해보면
$H(p, q) = -\sum_{i} p_{i}\; log\; q_{i} + \sum_{i} p_{i}\; log\; p_{i} + H(p)$
$= H(p)+\sum_{i} p_{i}\; log\; \cfrac{p_i}{q_i}$
여기서 뒤의 항 $\sum_{i} p_i\; log\; \cfrac{p_i}{q_i}$ 를 $\alpha$라고 가정하면 cross entropy $H(p, q)$를 전개한 것은 $H(p)$ 에서 $\alpha$라는 값이 더해진 것임을 알 수 있다. 이 $\alpha$가 확률 분포 $p$와 $q$의 정보량의 차이이며 이것이 바로 KL divergence 이다.
$\alpha$를 $KL(p||q)$로 표기하여 정리해보면, $KL(p||q) = H(p, q) - H(p)$ 임을 알 수 있다. 즉 KL divergence는 $p$와 $q$의 cross entropy에서 $p$의 entropy를 뺀 값이다. 그리고 KL divergence는 아래와 같이 표기한다.
$KL(p||q) = -\sum_i\; p_i \; log(\cfrac{q_i}{p_i})$
참조
[1] https://hyunw.kim/blog/2017/10/14/Entropy.html
'AI > Machine Learning' 카테고리의 다른 글
| 머신러닝 프로세스 (0) | 2023.08.01 |
|---|
댓글