AutoEncoder(오토 인코더)의 개념
AutoEncoder(AE)는 대표적인 비지도학습(Unsupervised-Learning) 신경망 모델이다. 기본적인 구조는 아래 그림과 같이 인코더(Encoder)와 디코더(Decoder)로 구성되어 있다. Input data에 대해 인코딩(압축)한 후 다시 원래 Input data로 디코딩(복원)하는 개념이다.

아래 그림에서 보면 Input data $x$에 4라는 이미지 값이 들어와 있고, 이 input을 인코더로 압축하여 $z$를 생성한다. 이 때, 이 $z$를 Latent Vector라고 부르며 Latent Vector는 input data를 압축하여 차원을 축소한 것으로 볼 수 있다. Input data의 차원이 잘 축소되었는지 확인하기 위해서 이를 다시 복원(reconstructing) 해야 한다. 따라서 $z$를 다시 디코더를 통하여 복원하여 출력 데이터 $x'$을 생성한 후, input data $x$와 output data $x'$이 같아지도록 네트워크를 훈련(training)하는 것이 AE의 기본 동작이라고 할 수 있다. 또한 여기서 Latent Vector, 즉 $z$는 새로운 feature로 사용할 수 있고 이 feature는 기존의 feature보다 차원(dimension)이 축소되었다는 장점이 있다.

AE의 목적
인코더와 디코더로 구성되어 있는 AE의 특성 상 두 가지 목적으로 구분할 수 있다.
첫 번째는 입력 데이터를 의미 있고 압축된 형태로 만들어주는 인코더를 학습 시키는 목적이 있다. 이를 AutoEncoder for manifold learnig 이라고 한다.
두 번째는 어떤 의미를 담고 있는 Latent Variable을 실제 데이터 분포로 만들어주는 디코더를 학습 시키는 목적이 있다. 이를 AutoEncoder for generative model 이라고 한다.
즉, AE는 데이터의 차원 축소와 생성 모델이라는 2가지 task로 구성되어 있다고 볼 수 있다.
차원 축소(Demensionality reduction)
Input data의 차원이 너무 크면, feature를 추출하기 어렵기 때문에 학습이 어려워진다. AE는 차원 축소의 기능을 하기 때문에 차원 축소를 통해 유용하게 활용할 수 있는 Classification, Clustering, Anomaly detection 등에 활용할 수 있다.
Lossy
Lossy는 직역하면 “손실되는” 이란 뜻으로 AE에서 Lossy는 output data의 퀄리티가 input data 보다 낮음을 의미한다. AE는 input data의 차원을 축소 하여 Latent Vector를 만들고 이를 복원하는 과정을 거쳐서 output을 input과 최대한 유사하게 만드는 방식으로 학습하기 때문에 input 보다 퀄리티가 낮을 수 밖에 없고, 이를 lossy라고 한다.
Manifold Learning
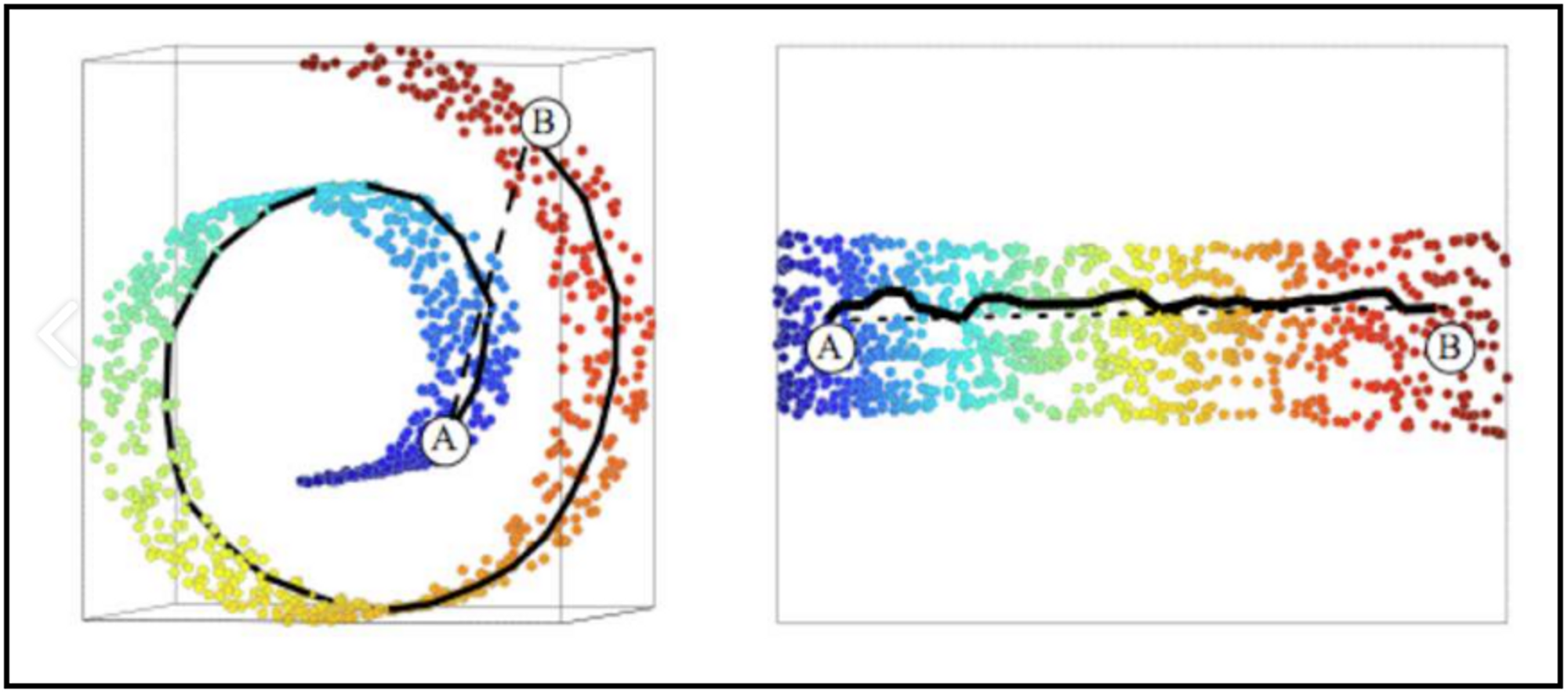
Manifold Learning은 차원 축소와 같은 의미이다. 그래서 AE의 궁극적인 목표는 Manifold Learning이라고도 할 수 있다. Manifold는 데이터가 있는 공간을 뜻한다. 아래 그림과 같이 3차원 상에 흩뿌려진 데이터가 있다고 할 때, 이를 아우르는 나선형의 평면이 있다. 이 나선형의 평면을 펼치면 2차원 평면이 된다. 3차원에서 2차원으로 차원이 축소되었으며, 이러한 평면을 찾는 방법이 Manifold Learning이다. 또한 여기서 3차원 상의 A와 B의 거리는 매우 가까워 보이지만 이를 2차원으로 펼치면 굉장히 멀리 있는 데이터가 된다. 이러한 문제점을 해결하기 위해서도 차원 축소가 필요한 것이다.
Manifold Learning의 목적
Minifold Learning, 차원 축소의 목적은 크게 4가지 이다.
- 데이터 압축 : 데이터를 압축한 뒤 압축한 Latent Vector를 다시 디코딩할 때, 원본 데이터로 복원이 제대로 된다면 압축이 잘 된 것이다.
- 데이터 시각화 : 차원이 높은 데이터는 시각화 하기 어렵다. 사람마다 다르다곤 하지만 나는 4차원 이상도 상상하기 매우 어렵다.
- 차원의 저주(Curse of Demension) 피하기 : 위의 Manifold 개념에 대한 예시가 차원의 저주에 관한 예시라고 할 수 있다. 또한 아래 그림처럼 1차원에서 3차원으로 데이터가 늘어날 때, 전체 공간을 차지하는 데이터 밀도를 유지하려면 데이터 개수가 매우 많아진다. 다시 말하면 데이터가 같을 때에는 차원이 늘수록 데이터 밀도가 급격히 줄어든다. 그러면 데이터의 특성을 잘 표현할 수 없다.

- 유용한 특징 추출 : Manifold를 찾았다는 것은 데이터에서 유용한 특징을 찾았다는 말과 같다. Manifold의 축에 따라 크기나 회전의 변화 등을 발견 할 수 있기 때문에 Manifold를 구하면 중요한 feature를 추출한 것과 같다.

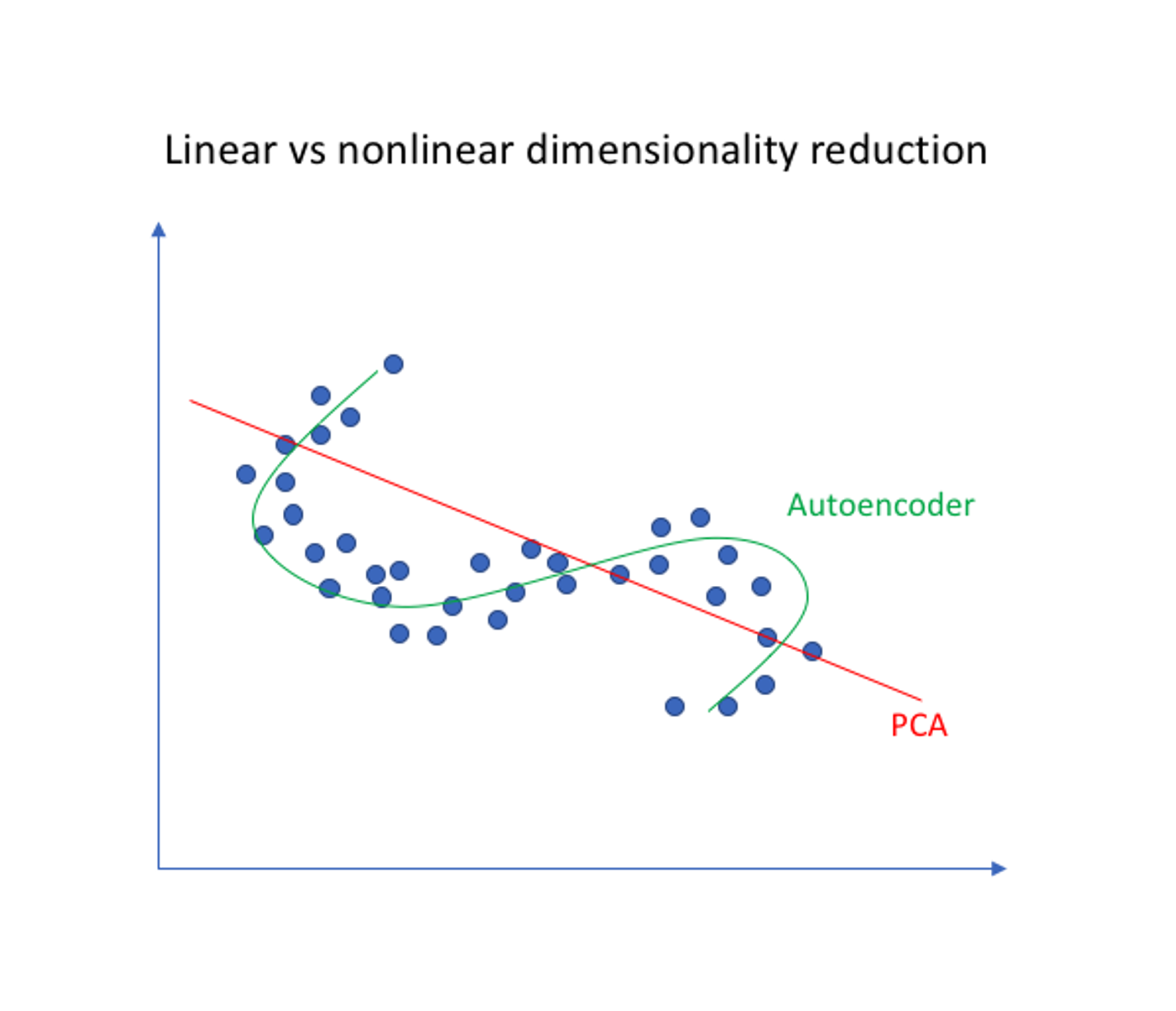
PCA와 AE의 차이점
AE뿐 아니라 PCA(Principal Component Analysis) 역시 차원 축소 방법이다. PCA는 hyperplane이라고도 하며 선형 차원 축소라면, AE는 비선형 차원 축소이다.
Loss function(손실 함수)
AE의 손실 함수는 간단하다. MSE와 Cross-entropy (데이터가 0과 1일 때) 를 사용한다.
MSE : $L(\theta) = \frac{1}{2}\sum_{k}||\hat{y}^k-x^k||_2^2 = \frac{1}{2} \sum_k \sum_i(\hat{y}_i^k-x_i^k)^2$
Cross-entropy : $L(\theta) = -\sum_k\{x^klog\;\hat{y}^k\ + (1-x^k)log(1-\hat{y}^k)\}$
아래와 같이 4라는 이미지의 input을 넣은 AE라면 output의 (1, 1) 픽셀과 target의 (1, 1) 픽셀의 MSE, 즉 1:1 대응이 되는 모든 픽셀의 MSE를 구해서 손실 함수를 구한다.

참조
[1] 오승상 교수님 유튜브 (딥러닝)
[2] 컴퓨터 비전 - 7. 오토인코더(AutoEncoder)와 매니폴드 학습(Manifold Learning) (tistory.com)
'AI > Deep Learning' 카테고리의 다른 글
| Activation function, 활성함수의 특징 (0) | 2024.11.30 |
|---|---|
| MLE 최대화가 Cross entropy 최소화와 같은 효과인 이유 (0) | 2024.11.30 |
| PSNR과 SSIM 설명 (1) | 2024.02.06 |
| Deep Neural Network (DNN) (0) | 2023.05.17 |
| 퍼셉트론(perceptron)과 Multilayer Perceptron(MLP) (0) | 2023.05.16 |
댓글